

Looking at the two graphs, we can see that the end behavior is different from what.
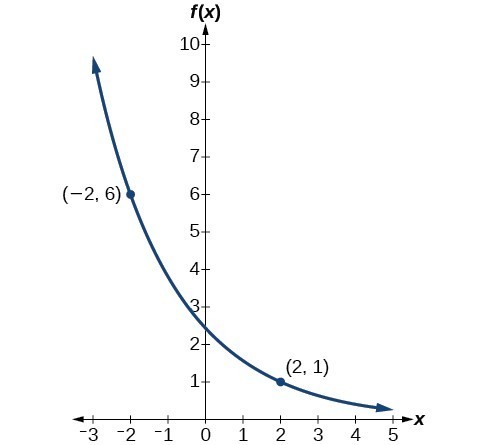
And so, the ratio between successive terms is going to be 1/7. Two possible shapes for the graph of an exponential function. And then if you think about it, every time you increase t by one, you're going to mulitply by 1/7 again. And so g(0), you could do that at time as being equal to zero if your t is time, would be equal to -2. Its domain is all real numbers and its range is all positive. Well, if t is equal to 0, then 1/7 to the zero power is 1. The math form f(x) ax defines Exponential Functions of base a if a is a positive real number. g(t) is going to be equal to our initial value, -2, times times our common ratio, 1/7, to the t power. So let me just write itĪgain a little bit neater. And we know that the common ratio is 1/7. Well, the fact that it'sĪn exponential function, we know that its formula is going to be of the form g(t) is equal to our initial value which we could call A, times our common ratio So, an initial value of -2, and a common ratio of 1/7, common ratio of 1/7. The graphs of exponential functions have two characteristic shapes, depending on whether the base, b, b, is greater than 1 1 or less than 1. The lower the x value, the nearer the curve. g is an exponential function with an initial value of -2. The following figure shows the coordinates plotted on the graph and connected by an arcing curve that swoops upward.


 0 kommentar(er)
0 kommentar(er)
